Oltre quarantamila euro raccolti al momento in cui scrivo e ancora 36 giorni di campagna utile a incrementare una tale cifra. Nasce da una collaborazione tra Regno Unito ed Italia, grazie alla sapienza progettuale della startup internettiana Atellani, l’ultimo inaspettato, stratosferico successo della piattaforma di finanziamenti online Kickstarter, frutto della fervida immaginazione dell’artista scultoreo Ivan Black. Nient’altro che uno dei più rinomati creativi nello specifico campo delle creazioni immaginifiche che siano non soltanto in grado di muoversi, grazie al vento, l’energia immessa dagli spettatori o ancora un semplice motore elettrico, bensì incoraggiate a farlo in funzione del messaggio estetico che possono comunicare: un apprezzamento indiretto e trasversale nei confronti della legge matematica di base. Quella che influenza, come noi sappiamo molto bene dal Rinascimento (per non parlare degli scritti di determinati filosofi e sapienti del Mondo Antico) l’essenza stessa del nostro posto dell’Universo, governando la composizione fisica delle cose inanimate, il verificarsi dei fenomeni atmosferici e persino il metodo e il funzionamento della vita stessa. Ma chi dovesse aspettarsi qualcosa di statico e noioso, nella presentazione immutabile del rapporto numerico noto come sezione aurea, sarà destinato a ricevere una piacevole sorpresa: poiché l’oggetto di quanto sin qui definito è in realtà l’oggetto informale e stravagante, sintetizzato da quel gesto all’apparenza quanto mai facèto, di far roteare in modo rapido le proprie svelte mani.
Utilizzi possibili, dunque, vediamo un po: c’è quello di stupire gli ospiti proprio quando la serata sembra assumere tinte noiose… Sfogare lo stress, nella maniera analoga a quella concessa dal classico yo-yo (e altri simili implementi). O perché no, tenere semplicemente occupate le mani, mentre si guarda una puntata della propria serie TV preferita su qualche sito di streaming con l’abbonamento mensile online. Certamente non particolarmente “utili” a meno che non si consideri tale il semplice ausilio che può offrire alla meditazione, benché il prezzo relativamente contenuto di 44-66 dollari (a seconda del colore a scelta tra bronzo, argento ed oro) sembrerebbe aver compensato le aspettative maggiormente irragionevoli e fuori luogo. Lasciando il posto alla capacità di apprezzare, semplicemente, l’opera di design di una firma di fama internazionale che, abbandonato momentaneamente il piedistallo dei propri significativi traguardi artistici, mette la propria mente al servizio del più puro e semplice divertimento, dietro un compenso unitario che potremmo definire chiaramente alla portata di chicchessia. E dire che, di precedenti insigni e degni di nota, il suo lungo curriculum ne possedeva più d’uno…
geometria
Il quadrato al centro della pizza e la divina vuvuzela
Secondo il teorema di Umbeltodt, occorre la commistione di tre fattori affinché il tempo possa piegarsi in maniera esponenziale, lasciando trascorrere quattro ore nel periodo soggettivo di circa 16 o 17 minuti. Punto primo, un gruppo di amici sufficientemente affiatati e armati di trombette sudamericane. Punto secondo, qualcosa di accattivante da guardare in televisione, diciamo ad esempio, una finale di campionato. E punto terzo, cibo in grado di solleticare le papille gustative di tutti i presenti, in quantità sufficiente da raggiungere la sazietà. Che tipo gioviale, quel Wolfram Umbeltodt! Un’ottima forchetta e grande appassionato di pallone. Tuttavia devoto, al di sopra di ogni altra cosa, al suo dovere di professore…. E puntuale in ogni cosa che faceva. Ragioni a causa delle quali mai e poi poteva capitargli, durante una delle sue serate d’alterazione spaziotemporale, di crollare addormentato sul più bello della situazione, sperimentando quel momento in bilico tra il sogno e la veglia, dove la logica cessa di condizionare l’esperienza umana. Causando, certe volte, l’esperienza transitoria dell’ispirazione.
Quanti di voi conoscono, d’altra parte, la figura iper-entusiastica di Clifford Stoll? L’astronomo, autore e professore del Lawrence Berkeley Laboratory, che dopo aver fatto della matematica una ragione di vita, si è dedicato al collezionismo di antiche calcolatrici meccaniche, la produzione in serie di bottiglie di vetro e le profezie non sempre esatte sul futuro catastrofico del mondo digitale. Un personaggio associato indissolubilmente, almeno per il popolo di Internet, al canale scientifico di Numberphile, dove presenta ad intervalli regolari curiosità scientifiche strettamente interconnesse ai temi ai lui più cari. Tra cui: l’applicazione dell’ogiva gaussiana ai monotoni strumenti musicali da stadio, piuttosto che il piatto italiano probabilmente più famoso al mondo. È uno strano approccio alla questione, il qui presente, sopratutto per il fatto che, qualora decidiamo d’interpretarlo in modo letterale, sembra distruttivo degli assiomi stessi alla base della nostra relazione con l’Universo. Già, la cosiddetta “geometria euclidea”. Quel sistema così antico e duraturo, nonostante le evidenti limitazioni, che per quasi 24 secoli avremmo potuto chiamarla semplicemente “la geometria”. Che riduce tutto ad una serie di precise connessioni, riuscendo in questo modo a dominare le nozioni stesse dell’esistenza. Eppure siamo qui riuniti, oggi, per prendere nota di un’inaspettata situazione: quella in cui, grazie alle condizioni idonee, ogni previsione smette di condizionare alcunché. Lasciando il posto a un nuovo tipo di poligoni: magnifici quadrati con cinque lati.
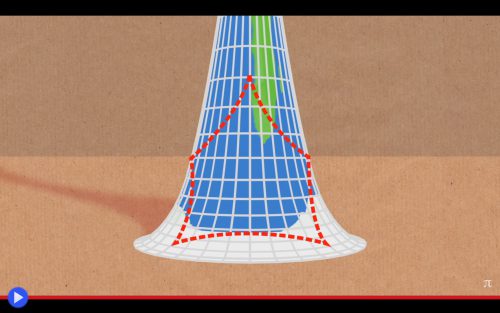
Riesco quasi ad udire le proteste dei tifosi sugli spalti, mentre l’apparente evidenza di quello che deve necessariamente essere un gioco di prestigio si presenta spontaneamente dinnanzi ai loro occhi, durante un concitato intermezzo di metà partita. Eppure, qualora si scelga di procedere per gradi, tutto sembra avere un senso. Prendiamo l’elemento di partenza, ovvero la fondamentale trombetta diventata celebre nel mondo durante i mondiali del 2014 tenuti in Brasile, per il suo suono terribilmente forte e monocorde. Ovviamente, voi non sentirete mai il buon Umbeltodt chiamarla Vuvuzela, bensì “Tromba dell’Arcangelo Gabriele”…. O per quanto concerne il professore americano dalla selvaggia chioma, beh, devo ammettere che non saprei dire. Ma sia chiaro che un simile nome, tanto altisonante e all’apparenza fuori luogo, è in realtà la reale definizione usata in geometria, per riferirsi all’esatta metà di una pseudosfera, che come aveva scoperto nel XVII secolo il matematico italiano Evangelista Torricelli (un nome, un programma) tende naturalmente all’infinito. Pur avendo un’area innegabilmente finita, tanto che si dice che la giusta quantità di vernice potrebbe ricoprire totalmente la sua superficie, a patto che possa essere “infinitamente diluita”. Paradossi a parte, è innegabile che esista una precisa caratteristica di un tale solido, se così scegliamo ancora di chiamarlo, particolarmente valida ad evidenziare l’effetto alla base dell’esperimento di Stoll: la sua capacità di essere convesso in ogni suo singolo punto. Modificando così profondamente l’interrelazione tra gli angoli e i segmenti, ovvero il concetto stesso della verità euclidea. Prima di addentrarci nel come tutto ciò possa accadere, direi che è giunto il momento di fare un piccolo snack…
Costruita sfera Pokemon per i biologi marini
Le più svariate motivazioni possono spingere qualcuno ad intraprendere il sentiero della scienza, tra le carriere più complesse, talvolta difficili e non sempre ricche d’immediate soddisfazioni. Può comunque causare un certo grado di stupore, la cognizione che al giorno d’oggi una di esse possa essere “Gotta catch’em all!” Ovvero lo slogan pubblicitario di un gioco elettronico che cambiò la storia di quel particolare media, dimostrando quanto fosse divertente catturare, far crescere e poi sfruttare in combattimento un grande numero di bestie immaginarie, tra il buffo, il fantastico e il mostruoso. Già, così tanto tempo è passato da quando Satoshi Tajiri, figlio di un venditore d’auto e una casalinga, dopo gli anni della sua rivista auto-prodotta sul media digitale interattivo ebbe modo di proporre a Nintendo un utilizzo mai pensato per prima per il cavo di collegamento del suo Gameboy: farci passare dentro insetti ed altre creature, affinché i bambini potessero “scambiarli” tra di loro. Era il 1996 ovvero abbastanza perché alcuni di coloro che crebbero facendo esattamente questo, oggi, siano dei ricercatori affermati nei rispettivi campi di competenza. Dove la realtà, talvolta, tende a superare di molto la fantasia. Che Zhi Ern Teoh, allora studente per il dottorato presso la prestigiosa divisione ingegneristica di Harvard, sia stato in precedenza un fan dei Pokémon dovrà per forza restare una mera speculazione. Nulla di simile è stato effettivamente dichiarato in alcuna intervista, conferenza stampa o biografia accademica. Tuttavia, è soprattutto osservando il frutto del suo lavoro, e in modo particolare l’utilizzo che quest’ultimo potrà riuscire ad avere sul campo, che la maggior parte dei siti Internet sembrano essere giunti alla stessa identica conclusione. Questo perché il RAD Sampler, l’apparato diventato oggetto dell’interesse collettivo proprio in questi giorni, a seguito della sua trattazione sulla rivista Science Robotics, sembra ricordare tanto da vicino l’orpello cardine dell’intera serie di videogiochi, giochi di carte e cartoni animati creata oltre due decadi fa. Molti dimenticano a tal proposito, seguendo in pieno il patto finzionale dell’autore, che il mondo dei mostri collezionabili non sia soltanto una fantasia di tipo biologico, ma anche e sopratutto purissima fantascienza. Nelle meccaniche di funzionamento della Pokéball (in italiano, sfera Poké) un attrezzo capace di “catturare” i mostriciattoli trasferendoli letteralmente in un universo quantistico parallelo. Come spiegare, altrimenti, il modo in cui un oggetto dal diametro approssimativo di una palla da tennis possa contenere draghi, pterodattili o giganteschi leviatani volanti? Ebbene io posso dirvi, con una certezza che proviene solamente dalla logica, che chiunque abbia cognizione di tutto questo, lavorando nel contempo in un qualsiasi campo di studio degli animali di questa Terra, un tale miracolo l’ha sognato più volte, come approccio super-semplice alla cattura di esemplari per la sua ricerca, soprattutto se appartenenti a specie difficili da maneggiare senza rischiare involontarie quanto problematiche conseguenze.
Sto parlando, per venire finalmente al nesso della questione, dell’opera di chi deve approcciarsi alle creature marine, per loro implicita natura alcune delle forme di vita più varie ed eclettiche del nostro pianeta. Il che sottintende che, per ogni pesce reso compatto dallo scheletro, molle cefalopode o mollusco corazzato, c’è una minuscola medusa predisposta a disgregarsi non appena viene toccata da mano umana, lasciandosi dietro il regno della materia osservabile e con esso, ogni proposito di essere attentamente studiata. Successe così che il giovane frequentatore della più famosa università statunitense, un giorno del 2014 scegliesse di partecipare a un corso del professore associato Chuck Hoberman dell’Istituto Wyss, divisione di Harvard deputata all’ingegneria ispirata ai processi naturali organici, nella quale si parlava di creare meccanismi capaci di piegarsi grazie a precisi calcoli matematici. Dal che lui scelse di elaborare, seguendo l’ispirazione del momento, un nuovo tipo di poliedri automatici, in cui l’applicazione di un singolo punto di pressione avrebbe indotto l’apertura, o chiusura del poligono di contenimento. L’idea di applicare una simile creazione nel campo della biologia marina, quindi, non sarebbe arrivata che qualche tempo topo, grazie al contributo di Brennan Phillips, un altro studente oggi assistente del dipartimento d’Ingegneria, il quale fece notare al suo collega quanto sarebbe stato utile poter disporre di un simile apparato per raccogliere campioni a notevoli profondità, in forza della sua semplicità di funzionamento, la quantità ridotta di parti mobili e la natura modulare del meccanismo. A quel punto il demone era metaforicamente fuori dalla bottiglia, il che poteva anche significare che c’era una bottiglia vuota, pronta ad accogliere le sopracitate, delicatissime meduse dei mari…
Il taglio che recide l’illusione del panino imperfetto
L’onnipresente legge del karma che dirige ogni azione del nostro essere, verso la ricerca di un modo per esprimere noi stessi di fronte all’indifferenza dell’universo? Tra l’incolore moltitudine della gente? Senza una ragione ulteriore, né reali propositi di guadagno personale: se voi riceveste, oggi stesso, il dono temporaneo dell’assoluta onnipotenza, sono pronto a scommettere che una delle vostre prime decisioni suonerebbe più o meno così: “Genio della lampada, per piacere. Risolvi subito il problema della fame del mondo.” Il che inevitabilmente, potrebbe implicare vie risolutive chiaramente distinte. A seconda del TIPO di approccio scelto dallo strumento della vostra volontà immanente. Ciò che intendo è che c’è sempre una strada alta (bombastica, estrema) ed una che ti porta a camminare sul fondo ombroso della valle (il Dio invisibile ma onnipresente) verso il raggiungimento dello stesso obiettivo. Che dunque potrebbero corrispondere, in tale specifico caso, in: 1 – Moltiplicazione dei pani e dei pesci, trasformazione dell’acqua in vino 2 – Equa divisione dei pani, dei pesci e del vino. È in effetti sorprendente quanti tra coloro che perseguono il Paradiso, attraverso una serie di virtù che includono l’altruismo e la carità, siano inerentemente inconsapevoli di come sia del tutto possibile, oggi come ieri, ottenere una divisione equa delle risorse per l’organismo coloniale che noi definiamo Pianeta Terra. L’unica cosa che ci servirebbe per farlo, è il dono dello sguardo assoluto. La capacità di dividere ogni cosa a metà. Come dite, non sempre questo è possibile? Un mero luogo comune, questo. Come postulò, per primo, il matematico polacco Hugo Steinhaus.
Il teorema del panino al prosciutto è una di quelle dimostrazioni matematiche che sembrano contro intuitive, ovvero palesemente scollegate dalla verità dei fatti, laddove in effetti pervadono ogni singolo recesso del nostro metodo per rapportarci all’esistenza. Esso afferma che, presi tre oggetti in uno spazio tridimensionale, è sempre possibile suddividerli in due metà perfettamente equivalenti con un singolo iperpiano dimensionale. Il che indica, in termini più immediatamente comprensibili e chiari, il singolo taglio di una katana. Ci scherza un po’ sopra, la dottoressa Hannah Fry nel suo nuovo video per il canale di YouTube Numberphile, evidenziando assieme alla voce fuori campo come un alto numero delle cognizioni matematiche più rilevanti sembrino essere nate all’interno delle caffetterie universitarie, come se il momento del pranzo fosse in effetti quello più produttivo nella giornata di questa intera categoria di scienziati. Ma questo è, di nuovo, riconducibile alla dottrina e i metodi meditativi di alcune correnti interne al buddhismo Mahayana. Meditazione Zen: comprendere il senso, mentre la mente è vuota. Nessuna preoccupazione, niente pensieri sull’immediato. Soltanto due fette di pane, non importa quanto frastagliate, ed una di prosciutto magari anche ripiegata su se stessa (il formaggio? Non pervenuto, mi spiace). E un tagliente coltello. Adesso immaginate la scena: lo stimato professore, già celebre per i grandi contributi al campo dell’analisi funzionale, che gira da un lato all’altro del tavolo, spostando di volta in volta questo o quel componente primario del suo umile pasto, mentre ne toglie e fagocita un pezzettino dopo l’altro. Rendendolo irregolare e spostandolo, perché se analizzate le implicazioni di una simile affermazione, “sempre possibile” comprenderete che i tre pezzi non dovranno trovarsi esattamente uno al di sopra dell’altro. Potranno anche essere in due piatti diversi. Diamine, potrebbero essere stati posizionati in degli UNIVERSI a incalcolabili anni luce di distanza (certo per tagliarli, a quel punto, servirebbe la forma finale di Gurren Lagann).
Ora, sarà importante specificare come, in effetti, la linea di ragionamento, suggerita da Steinhaus, per la prima volta in un diario ritrovato a decadi di distanza presso l’Università dell’Illinois, poi dimostrata formalmente da Arthur H. Stone e John Tukey, non fornisca in alcun modo gli strumenti necessari a trovare la posizione esatta del taglio. Tutto quello che può fare per noi, è rassicurarci sulla sua mera esistenza. Ma come direbbe il più grande e famoso dei samurai, Miyamoto Musashi, non è forse questo abbastanza per iniziare ad allenarci a cercarla? Tutto quello che occorre, è l’assoluta e indubitabile convinzione. Non soltanto il sospetto, che potremmo riassumere in: posso posizionare la lama in modo che il panino sia per il 100% da un lato. E posso farlo affinché sia per il 100% dall’altro. Dal che deriva… No, c’è un modo molto più esaustivo e totalizzante, per comprendere istantaneamente il teorema…