Situazione ricorrente nell’immaginario delle storie dei film d’arti marziali: il giovane guerriero si allontana dalla civiltà, per sfuggire alla crudele vendetta dei nemici del suo maestro, padre o signore. Per lunghi anni, a partire da quel fatidico momento, sopravvive spaccando legna, coltivando i frutti della terra e andando a caccia di conigli nella foresta. Ed è proprio nel coltivare il perfezionamento di un simile stile di vita, che diventa, progressivamente, il più perfetto degli spadaccini. Strane, indirette connessioni. Che attribuiscono alle attività più umili e mondane, il potere che permette di approcciarsi a una profonda, e duratura strada verso l’Illuminazione. Così come il professore di matematica, che approfondisce il significato più mistico e profondo dei suoi amici numeri, raggiunge il nesso al centro di quel nugolo di dati, ovvero la perfetta dimostrazione della tesi, di fronte al pubblico temporaneamente invisibile dei suoi studenti.
Ma sussiste nel contempo, in tutto questo, un certo quantitativo di abilità, sopratutto nel riempire quella liscia superficie nera dell’esatta quantità che fuoriesce, volta per volta, dai precisi conti frutto di un’intera carriera nel cifrario supremo che governa il regno dei concetti. Utilizzando, niente meno, che dei semplici gessetti. Ecco dunque, la ragione per cui ogni strumento utile a mantenere la propria concentrazione diventa, quasi subito, essenziale. Quanto lo tsuba che mantiene solida l’impugnatura della spada, così come l’acciaio hagane, ripiegato più e più volte su se stesso nella forgia infuocata di un fabbro di fama. Senza invocazioni alle Divine entità che risiedono nelle cose di tutti i giorni, è davvero possibile raggiungere lo stato ultimo dell’Eccellenza? Secondo l’opinione di molti creativi ed artigiani giapponesi, non proprio. Ed almeno giudicare dai risultati raggiunti attraverso gli oltre 50 anni di attività della sua azienda, a pieno titolo rientra in questo insieme Takayasu Watanabe ovvero l’uomo, pensionato dal 2015, che dall’immediato dopo guerra seppe fare del suo mestiere un’arte. E di quell’arte, una leggenda.
Immagino abbiate capito a questo punto ciò di cui stiamo parlando: niente più che semplice carbonato di calcio, risultante attraverso le epoche dalla disgregazione di scheletri e conchiglie, attentamente raccolto tramite metodologie industriali e poi spedito, come ingrediente principale, alla fabbrica di quel marchio celebre per molte generazioni, identificato caso vuole con il termine Hagoromo la connotazione della serie più ricca, Fulltouch. Ora si può fare molto, per custodire e amplificare una leggenda, senza entrare nel particolare di “che cosa”, esattamente, accresca i meriti di uno specifico quantum procedurale. Ma è senz’altro futile, a quel modo, perciò lasciate che vi ricordi brevemente le svariate problematiche degli anni della scuola: il rumore prodotto dallo scrivere sopra l’iconica lastra d’ardesia, con uno strumento che fa polvere, si sbriciola e disgrega. Che si spacca per mandare la punta delle vostre dita contro quella superficie liscia stridente, producendo un suono assai difficile da trascurare. E adesso immaginate quella stessa situazione d’incertezza, moltiplicata per i vasti spazi ricoperti per l’attività d’insegnamento di particolari branche della matematica, con continue interruzioni per sostituire l’attrezzo. C’è davvero da meravigliarsi, se i professori di una simile materia hanno fatto sempre tutto il possibile, per mandare avanti il nastro di un tale tiritera con il giusto acquisto, passando subito alla parte interessante della lezione?
matematica
Il quadrato al centro della pizza e la divina vuvuzela
Secondo il teorema di Umbeltodt, occorre la commistione di tre fattori affinché il tempo possa piegarsi in maniera esponenziale, lasciando trascorrere quattro ore nel periodo soggettivo di circa 16 o 17 minuti. Punto primo, un gruppo di amici sufficientemente affiatati e armati di trombette sudamericane. Punto secondo, qualcosa di accattivante da guardare in televisione, diciamo ad esempio, una finale di campionato. E punto terzo, cibo in grado di solleticare le papille gustative di tutti i presenti, in quantità sufficiente da raggiungere la sazietà. Che tipo gioviale, quel Wolfram Umbeltodt! Un’ottima forchetta e grande appassionato di pallone. Tuttavia devoto, al di sopra di ogni altra cosa, al suo dovere di professore…. E puntuale in ogni cosa che faceva. Ragioni a causa delle quali mai e poi poteva capitargli, durante una delle sue serate d’alterazione spaziotemporale, di crollare addormentato sul più bello della situazione, sperimentando quel momento in bilico tra il sogno e la veglia, dove la logica cessa di condizionare l’esperienza umana. Causando, certe volte, l’esperienza transitoria dell’ispirazione.
Quanti di voi conoscono, d’altra parte, la figura iper-entusiastica di Clifford Stoll? L’astronomo, autore e professore del Lawrence Berkeley Laboratory, che dopo aver fatto della matematica una ragione di vita, si è dedicato al collezionismo di antiche calcolatrici meccaniche, la produzione in serie di bottiglie di vetro e le profezie non sempre esatte sul futuro catastrofico del mondo digitale. Un personaggio associato indissolubilmente, almeno per il popolo di Internet, al canale scientifico di Numberphile, dove presenta ad intervalli regolari curiosità scientifiche strettamente interconnesse ai temi ai lui più cari. Tra cui: l’applicazione dell’ogiva gaussiana ai monotoni strumenti musicali da stadio, piuttosto che il piatto italiano probabilmente più famoso al mondo. È uno strano approccio alla questione, il qui presente, sopratutto per il fatto che, qualora decidiamo d’interpretarlo in modo letterale, sembra distruttivo degli assiomi stessi alla base della nostra relazione con l’Universo. Già, la cosiddetta “geometria euclidea”. Quel sistema così antico e duraturo, nonostante le evidenti limitazioni, che per quasi 24 secoli avremmo potuto chiamarla semplicemente “la geometria”. Che riduce tutto ad una serie di precise connessioni, riuscendo in questo modo a dominare le nozioni stesse dell’esistenza. Eppure siamo qui riuniti, oggi, per prendere nota di un’inaspettata situazione: quella in cui, grazie alle condizioni idonee, ogni previsione smette di condizionare alcunché. Lasciando il posto a un nuovo tipo di poligoni: magnifici quadrati con cinque lati.
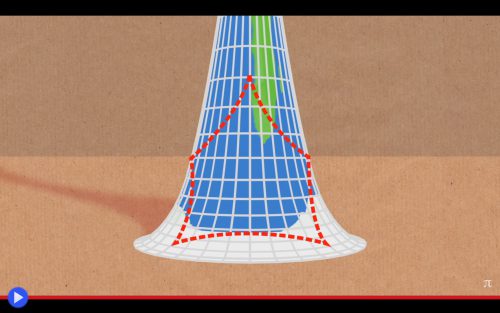
Riesco quasi ad udire le proteste dei tifosi sugli spalti, mentre l’apparente evidenza di quello che deve necessariamente essere un gioco di prestigio si presenta spontaneamente dinnanzi ai loro occhi, durante un concitato intermezzo di metà partita. Eppure, qualora si scelga di procedere per gradi, tutto sembra avere un senso. Prendiamo l’elemento di partenza, ovvero la fondamentale trombetta diventata celebre nel mondo durante i mondiali del 2014 tenuti in Brasile, per il suo suono terribilmente forte e monocorde. Ovviamente, voi non sentirete mai il buon Umbeltodt chiamarla Vuvuzela, bensì “Tromba dell’Arcangelo Gabriele”…. O per quanto concerne il professore americano dalla selvaggia chioma, beh, devo ammettere che non saprei dire. Ma sia chiaro che un simile nome, tanto altisonante e all’apparenza fuori luogo, è in realtà la reale definizione usata in geometria, per riferirsi all’esatta metà di una pseudosfera, che come aveva scoperto nel XVII secolo il matematico italiano Evangelista Torricelli (un nome, un programma) tende naturalmente all’infinito. Pur avendo un’area innegabilmente finita, tanto che si dice che la giusta quantità di vernice potrebbe ricoprire totalmente la sua superficie, a patto che possa essere “infinitamente diluita”. Paradossi a parte, è innegabile che esista una precisa caratteristica di un tale solido, se così scegliamo ancora di chiamarlo, particolarmente valida ad evidenziare l’effetto alla base dell’esperimento di Stoll: la sua capacità di essere convesso in ogni suo singolo punto. Modificando così profondamente l’interrelazione tra gli angoli e i segmenti, ovvero il concetto stesso della verità euclidea. Prima di addentrarci nel come tutto ciò possa accadere, direi che è giunto il momento di fare un piccolo snack…
Il taglio che recide l’illusione del panino imperfetto
L’onnipresente legge del karma che dirige ogni azione del nostro essere, verso la ricerca di un modo per esprimere noi stessi di fronte all’indifferenza dell’universo? Tra l’incolore moltitudine della gente? Senza una ragione ulteriore, né reali propositi di guadagno personale: se voi riceveste, oggi stesso, il dono temporaneo dell’assoluta onnipotenza, sono pronto a scommettere che una delle vostre prime decisioni suonerebbe più o meno così: “Genio della lampada, per piacere. Risolvi subito il problema della fame del mondo.” Il che inevitabilmente, potrebbe implicare vie risolutive chiaramente distinte. A seconda del TIPO di approccio scelto dallo strumento della vostra volontà immanente. Ciò che intendo è che c’è sempre una strada alta (bombastica, estrema) ed una che ti porta a camminare sul fondo ombroso della valle (il Dio invisibile ma onnipresente) verso il raggiungimento dello stesso obiettivo. Che dunque potrebbero corrispondere, in tale specifico caso, in: 1 – Moltiplicazione dei pani e dei pesci, trasformazione dell’acqua in vino 2 – Equa divisione dei pani, dei pesci e del vino. È in effetti sorprendente quanti tra coloro che perseguono il Paradiso, attraverso una serie di virtù che includono l’altruismo e la carità, siano inerentemente inconsapevoli di come sia del tutto possibile, oggi come ieri, ottenere una divisione equa delle risorse per l’organismo coloniale che noi definiamo Pianeta Terra. L’unica cosa che ci servirebbe per farlo, è il dono dello sguardo assoluto. La capacità di dividere ogni cosa a metà. Come dite, non sempre questo è possibile? Un mero luogo comune, questo. Come postulò, per primo, il matematico polacco Hugo Steinhaus.
Il teorema del panino al prosciutto è una di quelle dimostrazioni matematiche che sembrano contro intuitive, ovvero palesemente scollegate dalla verità dei fatti, laddove in effetti pervadono ogni singolo recesso del nostro metodo per rapportarci all’esistenza. Esso afferma che, presi tre oggetti in uno spazio tridimensionale, è sempre possibile suddividerli in due metà perfettamente equivalenti con un singolo iperpiano dimensionale. Il che indica, in termini più immediatamente comprensibili e chiari, il singolo taglio di una katana. Ci scherza un po’ sopra, la dottoressa Hannah Fry nel suo nuovo video per il canale di YouTube Numberphile, evidenziando assieme alla voce fuori campo come un alto numero delle cognizioni matematiche più rilevanti sembrino essere nate all’interno delle caffetterie universitarie, come se il momento del pranzo fosse in effetti quello più produttivo nella giornata di questa intera categoria di scienziati. Ma questo è, di nuovo, riconducibile alla dottrina e i metodi meditativi di alcune correnti interne al buddhismo Mahayana. Meditazione Zen: comprendere il senso, mentre la mente è vuota. Nessuna preoccupazione, niente pensieri sull’immediato. Soltanto due fette di pane, non importa quanto frastagliate, ed una di prosciutto magari anche ripiegata su se stessa (il formaggio? Non pervenuto, mi spiace). E un tagliente coltello. Adesso immaginate la scena: lo stimato professore, già celebre per i grandi contributi al campo dell’analisi funzionale, che gira da un lato all’altro del tavolo, spostando di volta in volta questo o quel componente primario del suo umile pasto, mentre ne toglie e fagocita un pezzettino dopo l’altro. Rendendolo irregolare e spostandolo, perché se analizzate le implicazioni di una simile affermazione, “sempre possibile” comprenderete che i tre pezzi non dovranno trovarsi esattamente uno al di sopra dell’altro. Potranno anche essere in due piatti diversi. Diamine, potrebbero essere stati posizionati in degli UNIVERSI a incalcolabili anni luce di distanza (certo per tagliarli, a quel punto, servirebbe la forma finale di Gurren Lagann).
Ora, sarà importante specificare come, in effetti, la linea di ragionamento, suggerita da Steinhaus, per la prima volta in un diario ritrovato a decadi di distanza presso l’Università dell’Illinois, poi dimostrata formalmente da Arthur H. Stone e John Tukey, non fornisca in alcun modo gli strumenti necessari a trovare la posizione esatta del taglio. Tutto quello che può fare per noi, è rassicurarci sulla sua mera esistenza. Ma come direbbe il più grande e famoso dei samurai, Miyamoto Musashi, non è forse questo abbastanza per iniziare ad allenarci a cercarla? Tutto quello che occorre, è l’assoluta e indubitabile convinzione. Non soltanto il sospetto, che potremmo riassumere in: posso posizionare la lama in modo che il panino sia per il 100% da un lato. E posso farlo affinché sia per il 100% dall’altro. Dal che deriva… No, c’è un modo molto più esaustivo e totalizzante, per comprendere istantaneamente il teorema…
Le illusioni ottiche perdute del creatore dei cilindri ambigui
Un’automobilina gialla è parcheggiata al sicuro sotto la sua piccola tettoia, dall’apparente forma di un rettangolo convesso o sezione di un cilindro che dir si voglia. Ma basta osservare la scena allo specchio, per scoprire una visione alternativa della realtà: la struttura assume la forma, a quanto pare, di un paravento disposto a zig-zag, decisamente meno utile a far scivolare via la pioggia… Qual’è dunque la realtà, l’una oppure l’altra delle due visioni? O magari la più improbabile via di mezzo tra le due? Nel proseguire della carrellata, un cerchio che rappresenta la luna viene fatto ruotare su se stesso. Raggiunta la posizione dei 180°, esso diventa all’improvviso…Una stella! Un fiore si trasforma in farfalla. Una bottiglia di vino, in bicchiere. È difficile, raggiunto un tale punto, immaginare quale sia il segreto di quest’uomo…
Si, potremmo chiederlo alla Francia, in forza della conclusione dei recenti Europei di calcio: vincere non è facile, ma ciò che costa veramente fatica, alla fin fine della fiera, è giungere secondi nell’assegnazione degli onori del torneo. Perché se è vero che hanno inventato quella cosa, il podio che è struttura metaforica e/o effettivamente calpestabile (ne vedremo molti laggiù a Rio) va anche detto che posizionarsi sui due cubi laterali comporta quasi sempre un senso di rimpianto inalienabile, ricolmo del “forse avrei dovuto fare la tale cosa” oppure “perché mai ho scelto di rispondere a quel modo!” La strategia: un punto fondamentale degli sport, siano questi di squadra oppure individuali, il valore oggettivo che condiziona l’esito della disfida. Mentre diverso è il caso di una gara che, per quanto prestigiosa, comporta la selezione di un qualcosa di creativo. L’àmbito contestuale, da che il mondo è tondo, dell’assoluta soggettività dell’individuo, che seleziona sempre ciò che maggiormente colpisce il SUO modo di vedere le cose e l’Universo, la SUA inclinazione perfettamente personale. Il che ci porterebbe a chiederci, in ultima analisi, a cosa serva l’annuale competizione “Illusione dell’Anno” che si tiene presso il Centro Filarmonico delle Arti di Naples, in Florida, con lo scopo di premiare colui o colei che ha saputo dimostrare la migliore capacità di trarre in inganno le pupille ed i neuroni degli umani. Quando è chiaro che persino la giuria più esperta, in ultima analisi, non potrà che far classifica di ciò che in quel particolare momento, tutto considerato, gli è sembrato maggiormente fantasioso, creativo, originale. Se poi si dovesse addirittura decidere di far votare i migliori tra i finalisti al “grande pubblico” attraverso un semplice sondaggio online, come orgogliosamente dichiarato dall’organizzatrice dell’evento, la Neural Correlate Society, allora apriti cielo!
Disinteressato, spontaneo, sincero: tre meriti che l’utente medio di Internet, pur possedendoli nella sua vita reale, tende a non mostrare in ciò che clicca e tenta di portare alle più estreme conseguenze. Così è capitato che quest’anno, al termine della prestigiosa kernesse, una proposta visivamente sorprendente come quella dei “cilindri ambigui” di Kokichi Sugihara, professore di matematica all’Università Meiji di Tokyo, siano giunti dietro a una realizzazione che si è rivelata secondo l’evidente opinione dell’ancor più grande prova popolare, a conti fatti, molto meno significativa. Intendiamoci, non si può certo dire che la breve sequenza di Mathew T. Harrison e Gideon P. Caplovitz dell’Università del Nevada, intitolata “Motion Integration Unleashed: New Tricks for an Old Dog” sia stata priva d’interesse o meriti di sorta. E i loro gabors in traslazione, pallini astratti in grado d’ingannare l’occhio con il movimento interno di un pattern, certamente avranno stupito più di un occhio ed un cervello privi di alcun preconcetto pre-esistente. Ma quando la maggior parte dei blog mondiali, Reddit e persino alcuni quotidiani online di fama, pubblicano un raro articolo sulla gara (più che altro per mostrarne i video) ponendo nel titolo non il primo, ma il secondo classificato…È chiaro che qualcosa non è andato per il verso giusto.