Secondo il teorema di Umbeltodt, occorre la commistione di tre fattori affinché il tempo possa piegarsi in maniera esponenziale, lasciando trascorrere quattro ore nel periodo soggettivo di circa 16 o 17 minuti. Punto primo, un gruppo di amici sufficientemente affiatati e armati di trombette sudamericane. Punto secondo, qualcosa di accattivante da guardare in televisione, diciamo ad esempio, una finale di campionato. E punto terzo, cibo in grado di solleticare le papille gustative di tutti i presenti, in quantità sufficiente da raggiungere la sazietà. Che tipo gioviale, quel Wolfram Umbeltodt! Un’ottima forchetta e grande appassionato di pallone. Tuttavia devoto, al di sopra di ogni altra cosa, al suo dovere di professore…. E puntuale in ogni cosa che faceva. Ragioni a causa delle quali mai e poi poteva capitargli, durante una delle sue serate d’alterazione spaziotemporale, di crollare addormentato sul più bello della situazione, sperimentando quel momento in bilico tra il sogno e la veglia, dove la logica cessa di condizionare l’esperienza umana. Causando, certe volte, l’esperienza transitoria dell’ispirazione.
Quanti di voi conoscono, d’altra parte, la figura iper-entusiastica di Clifford Stoll? L’astronomo, autore e professore del Lawrence Berkeley Laboratory, che dopo aver fatto della matematica una ragione di vita, si è dedicato al collezionismo di antiche calcolatrici meccaniche, la produzione in serie di bottiglie di vetro e le profezie non sempre esatte sul futuro catastrofico del mondo digitale. Un personaggio associato indissolubilmente, almeno per il popolo di Internet, al canale scientifico di Numberphile, dove presenta ad intervalli regolari curiosità scientifiche strettamente interconnesse ai temi ai lui più cari. Tra cui: l’applicazione dell’ogiva gaussiana ai monotoni strumenti musicali da stadio, piuttosto che il piatto italiano probabilmente più famoso al mondo. È uno strano approccio alla questione, il qui presente, sopratutto per il fatto che, qualora decidiamo d’interpretarlo in modo letterale, sembra distruttivo degli assiomi stessi alla base della nostra relazione con l’Universo. Già, la cosiddetta “geometria euclidea”. Quel sistema così antico e duraturo, nonostante le evidenti limitazioni, che per quasi 24 secoli avremmo potuto chiamarla semplicemente “la geometria”. Che riduce tutto ad una serie di precise connessioni, riuscendo in questo modo a dominare le nozioni stesse dell’esistenza. Eppure siamo qui riuniti, oggi, per prendere nota di un’inaspettata situazione: quella in cui, grazie alle condizioni idonee, ogni previsione smette di condizionare alcunché. Lasciando il posto a un nuovo tipo di poligoni: magnifici quadrati con cinque lati.
Riesco quasi ad udire le proteste dei tifosi sugli spalti, mentre l’apparente evidenza di quello che deve necessariamente essere un gioco di prestigio si presenta spontaneamente dinnanzi ai loro occhi, durante un concitato intermezzo di metà partita. Eppure, qualora si scelga di procedere per gradi, tutto sembra avere un senso. Prendiamo l’elemento di partenza, ovvero la fondamentale trombetta diventata celebre nel mondo durante i mondiali del 2014 tenuti in Brasile, per il suo suono terribilmente forte e monocorde. Ovviamente, voi non sentirete mai il buon Umbeltodt chiamarla Vuvuzela, bensì “Tromba dell’Arcangelo Gabriele”…. O per quanto concerne il professore americano dalla selvaggia chioma, beh, devo ammettere che non saprei dire. Ma sia chiaro che un simile nome, tanto altisonante e all’apparenza fuori luogo, è in realtà la reale definizione usata in geometria, per riferirsi all’esatta metà di una pseudosfera, che come aveva scoperto nel XVII secolo il matematico italiano Evangelista Torricelli (un nome, un programma) tende naturalmente all’infinito. Pur avendo un’area innegabilmente finita, tanto che si dice che la giusta quantità di vernice potrebbe ricoprire totalmente la sua superficie, a patto che possa essere “infinitamente diluita”. Paradossi a parte, è innegabile che esista una precisa caratteristica di un tale solido, se così scegliamo ancora di chiamarlo, particolarmente valida ad evidenziare l’effetto alla base dell’esperimento di Stoll: la sua capacità di essere convesso in ogni suo singolo punto. Modificando così profondamente l’interrelazione tra gli angoli e i segmenti, ovvero il concetto stesso della verità euclidea. Prima di addentrarci nel come tutto ciò possa accadere, direi che è giunto il momento di fare un piccolo snack…
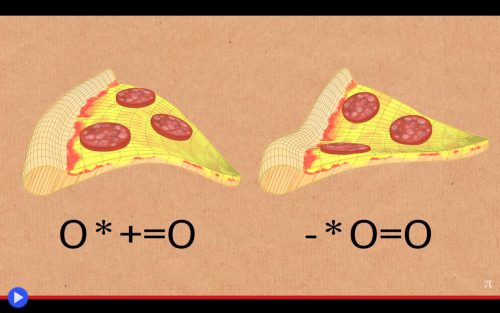
Ed è qui che entra in gioco, immancabilmente ad ogni esposizione, quell’ennesimo nome da noi fin soltanto citato di sfuggita, del Princeps mathematicorum, che ebbe in vita il nome di Carl Friedrich Gauss. I cui studi sulla cartografia condotti verso il primo terzo del XIX secolo avrebbe portato, con sua stessa estrema sorpresa, all’elaborazione di ciò che era destinato a prendere il nome di teorema egregium (nessuno potrebbe negare che all’epoca andassero di moda i superlativi latini) secondo cui: “La curvatura è una proprietà intrinseca delle superfici, indipendente dal modo in cui vengono immerse in uno spazio tridimensionale”. Tornando dunque a noi, ovvero al video che il buon Stoll aveva pubblicato originariamente nel 2016, nel quale si barcamenava nel gestire una fetta triangolare di pizza, chiedendosi perché, fin dall’epoca della nostra infanzia, ci sia stato insegnato a tenerla in quel particolare modo. Ovvero con i due vertici per così dire posteriori, ripiegati verso l’alto, ben sapendo che in quel modo il condimento non cadrà in avanti… E perché mai, volendo essere pignoli, succede tutto questo?! La risposta è da ricercarsi nell’interazione tra due curve, l’una intrinseca, l’altra indotta da noi stessi durante il pasto. Secondo l’eccelso teorema infatti, ogni fetta di pizza disposta sopra un piano possiede una curvatura di partenza pari a zero… Che non potrà mai essere eliminata in alcun modo! Mentre nel momento stesso in cui la si solleva, essa dovrà acquisirne una ulteriore, che può essere sia positiva che negativa. Immaginate, a tal proposito, il gesto compiuto arrotolando su se stesso un foglio di carta con sopra disegnate due linee rette perpendicolari: è innegabile che quella longitudinale sia destinata a guadagnare, così facendo, una curvatura di tipo positivo (convessa) o nel caso in cui la croce disegnata sia mantenuta all’interno, di tipo negativo (concava). Ma la sua compagna resterà, dal canto suo, rigorosamente al valore zero. E dato che due curvature, al momento in cui s’incontrano, moltiplicano vicendevolmente i propri effetti, c’è un solo effetto possibile che possa risultare da questo incontro di fattori: qualsiasi cifra, non importa se positiva o negativa, quando viene moltiplicata per zero dà… Zero. Ed è per questo che la pizza non potrà, mai e poi mai, piegarsi in avanti.
Facendo dunque un balzo rapido al 2018, e al nuovo corollario della tromba dell’arcangelo o il tifoso sudamericano che dir si voglia, che cosa avviene quando si prende in considerazione un solido la cui curvatura innata resterà sempre e soltanto positiva, piuttosto che neutrale? Perché guardate, è esattamente questo che succede nel caso di tutte le pseudosfere, non importa quale aspetto si scelga di analizzare per primo: questi prodotti della rotazione di un trattrice attorno all’asintoto (ehm… prendetela per buona) che non producono alcun tipo di circonferenza che possa presentare la curva gaussiana dal valore zero, da contrapporsi a quello positivo della forma naturalmente convessa di alcunché. Bensì soltanto una quantità potenzialmente infinita di assi, ciascuno dei quali può essere soltanto positivo o negativo. Moltiplicando i quali a vicenda, si ottiene prevedibilmente una cifra sempre superiore allo zero. Ed è qui, signori miei, che le vostre aspettative in merito alle regole di questo mondo finiscono per essere completamente sovvertite…

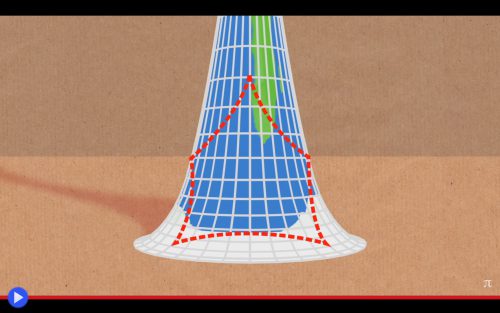
È scontato che perché l’astuta teoria presentata in video da Cliff Stoll funzioni, occorre accettare la sua definizione di cosa sia, effettivamente, un quadrato. Una volta fuoriusciti dalle regole dello spazio bidimensionale (euclideo) del resto, sussiste un certo grado di libera interpretazione in merito a simili idee. Il quadrilatero che tutti amiamo, in questo caso diventerebbe dunque “il poligono definito da quattro angoli retti a 90 gradi”. Detto ciò, ed è chiaro che in qualsiasi postulato matematico, la parola debba diventare verità, il professore inizia dunque a tracciare gli angoli sulla trombetta, senza particolari esitazioni. Definisce il primo, poi il secondo, il terzo ed il quarto. A quel punto mette l’oggetto dinnanzi alla telecamera: molto evidentemente, ne manca uno. Mentre il suo sorriso si allarga ancora e ancora, dunque, ne traccia un altro: ecco qui, le jeux sont faits: un “quadrato” a cinque lati. Qualcuno potrebbe scegliere di chiamarlo un pentagono. Pur così facendo, d’altra parte, non potrebbe negare che ha soltanto angoli retti.
Come è possibile tutto questo? La risposta è che NON è possibile, per lo meno qualora si scelga di accettare gli assiomi della geometria euclidea, come fatto dall’intera civilizzazione umana a partire da quell’epoca remota in cui il primo geometra del mondo, saziando le aspettative dei suoi contemporanei, pubblicò il suo capolavoro Στοιχεῖα (Stoichêia – gli Elementi). Ed infatti nel momento stesso in cui Stoll tenta scherzosamente di appiattire un foglio di carta corrispondente al quadrato magico sul proprio tavolo, appare evidente la maniera in cui ciascuno dei suoi vertici tenti di sfuggire verso l’alto, o alternativamente, la superficie impenetrabile del legno sottostante. Se costretto a conformarsi mediante l’impiego di una pressa, tale foglio in effetti si strapperebbe di sicuro, perdendo ogni residua qualità inerente. Qualcosa di simile a quello che avviene con le nostre certezze, ogni qualvolta si tenti di introdurre in una discussione concetti come i viaggi del tempo, o gli infiniti universi paralleli.
La vita è davvero strana, in fin dei conti. Pensate che esiste un luogo in cui mettono l’ananas sulla pizza. E il suono penetrante della vuvuzela, piuttosto che agitare gli animi, ha un effetto calmante. Un giorno, prima o poi, il Prof. Umbeltodt cadrà addormentato, con un bicchiere di birra in mano. Per visitarlo anche lui, sul finire di una giornata di lunghissime lezioni, pasti fuori dallo spaziotempo e severe pallonate che raggiungono l’incrocio dei pali.